Research
My research involves a lot of astrophysical simulations that are too large to fit into a single computer. Well, in principle they can if you have unlimited patience and don't mind swapping between memory and hard disk back and forth! Instead, I would have to divide each simulation into multiple pieces and run them in parallel in computing clusters.
The simulations I run are called "N-body" simulations, where N particles interact with all the others by their mutual gravity. When N > 2 (for me N is anywhere from 104 to 109) a problem like that has to be solved numerically step-by-step in time. Every simulation output has at least 6 dimensions: 3 for position, and 3 for velocity. There are many existing codes that run N-body simulations, so my work is to understand what we are trying to simulate, set it up, and analyze the results.
Here is a bit of context...
The ΛCDM universe on small scales
The ΛCDM (or "lambda-cold-dark-matter") model has been widely successful in describing the universe on large scales. But on small scales, one model prediction that still hasn't been verified is that the dark matter halo of a Milky-Way-sized galaxy isn't smooth, but contains a lot of bound clumps called "subhalos". Because each subhalo should be less than 0.1% of the mass of the Milky Way and is probably made of entirely dark matter, it's very difficult to tell if they exist. Finding evidence for the subhalos' existence is a very important step to understand what dark matter is.
Tidal streams: Basics
When a small cluster of stars (e.g. a globular cluster or a dwarf galaxy) orbits around its host galaxy, the galaxy's tidal field would stretch the star cluster into a long stream that wraps around the galaxy. These "tidal streams" are a promising tool to see if subhalos exist.
Imagine a streams of stars lined up one after another. If at some point this stream encountered a subhalo, the subhalo's gravity would knock out some stars along the stream at the point of the impact, and this would show up as a little "gap" in the stream. My computer simulations show that streams in a galaxy with and without subhalos look very different (Ngan & Carlberg, 2014). This tells us that gaps in tidal streams can be convincing evidence for the subhalos' existence.
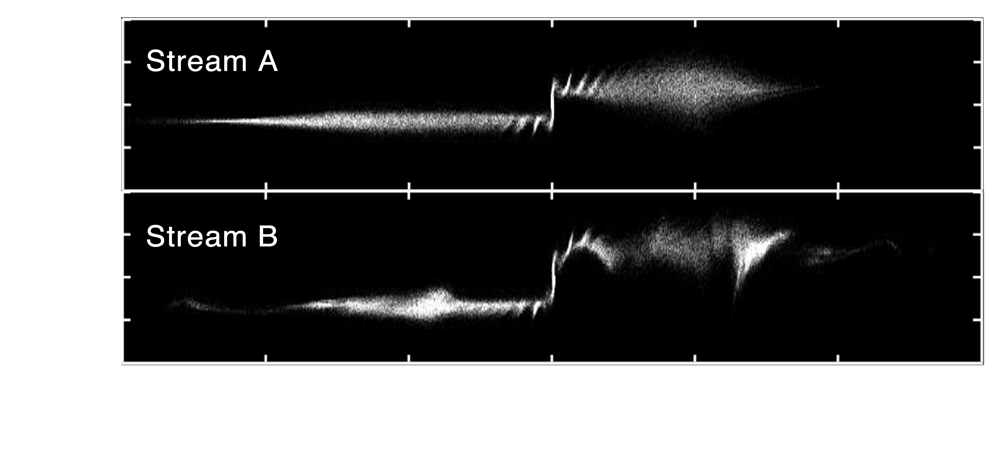
Two tidal streams with their curvatures subtracted. Stream A orbits in a galaxy that has no subhalos, while Stream B orbits in a galaxy that has the subhalos as predicted by the ΛCDM model.
(Taken from Ngan & Carlberg, 2014)
Tidal streams: In reality
Most studies to date, including my own above, used some sort of approximation for the host galaxy's gravity. Approximations simplify computations, and the results are easier to understand, at the cost of realism. Sometimes this cost is negligible, but for tidal streams it probably isn't.
Learning what the Milky Way's dark matter halo actually looks like is a topic of ongoing research, but we already have some rough ideas. Some previous simulations used billions of particles to simulate a large part of the universe, which allowed us to study how dark matter halos form in detail. The output of a "cosmological" simulation like that gives us a realistic dark matter halo, represented by billions of particles.
Computing the gravity inside a realistic halo is not easy because we are no longer using approximations, but it can be done with a few special tricks (Ngan et al, 2015). Here is how different tidal streams would look like when their halos' gravity is computed approximately vs realistically:


Top: 50 tidal streams projected onto the sky. They are simulated using an approximate way to compute the halo's gravity.
Bottom: Same as the top but using a realistic halo. The streams are much more dispersed.
(Taken from Ngan et al, 2016)
The streams in the approximate halo (top) are a lot skinnier than the streams in the realistic halo (bottom). This is expected because the approximation is so simple, there isn't much else the stars in a stream can do other than going one after another, so they would just line up roughly in the same track. On the other hand, a realistic halo gives the stars in a stream more freedom to move away from the stream's track.
So what does this result mean? Is there any point in using the approximate halo to simulate tidal streams? We're not sure yet. At the time of writing, the effect of a realistic halo on tidal streams has only been explored recently, so ongoing research will tell us more.